NATURAL FREQUENCY VEERING IN PLANETARY GEARS
ABSTRACT
To achieve noise and vibration reduction in planetary gear applications, key design parameters are often varied to avoid resonances,optimize load distribution, and reduce weight. In the plots of natural frequencies versus planetary gear parameters,veering phenomena occur when two eigenvalue loci approach each other, but then abruptly veer away. The importance of veering is manifested in the dramatic changes in the vibration modes of the veering natural frequencies and the consequent impact on response.This work analytically characterizes the rules of eigenvalue veering in planetary gears.The coupling factors between two close eigenvalue loci are approximated by perturbation analysis. Special veering patterns were obtained using the unique properties of planetary gear vibration modes.The results are illustrated by an example. Key design parameters were investigated, and generalized guidance is provided for tuning planetary gear natural frequencies.
I. INTRODUCTION
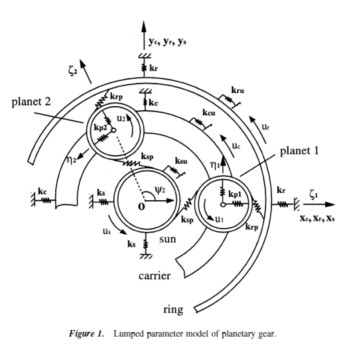
Noise and vibration reduction are critical concerns in planetary gear applications. During the design process, system parameters are varied to evaluate alternative design choices,avoid resonances,optimize load distribution,and reduce weight. It is important to characterize the effects of parameter variations on the natural frequencies and vibration modes for effective vibration tuning. In planetary gear dynamic models (Fig. 1), the key design parameters include the mesh stiffnesses, support/bearing stiffnesses, component masses, and moments of inertia. Some plots of natural frequencies versus planetary gear parameters are presented by Cunliffe et al. [1], Botman [2], Kahraman [3,4], and Saada and Velex [5].
Natural frequency plots in these studies, especially Ref. 3, show natural
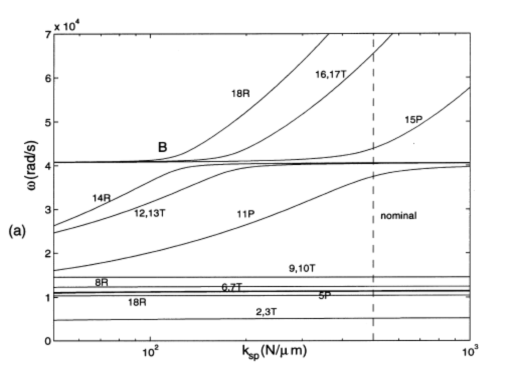
frequency veering phenomena when two eigenvalue loci approach each other as a parameter is varied, but then abruptly veer away like two similar charges repelling (point B in Fig. 2a). The vibration modes of the veering eigenvalues are strongly coupled and undergo dramatic changes in the veering neighborhood.The phenomenon has been studied extensively [6–9], but it has not been explored in planetary gears.Eigenvalue veering is also related to mode localization that can occur when disorder is introduced into nominally symmetric systems like turbine blades, space antennae, multispan beams, and other structures [6]. In the case of especially sharp veering, it is sometimes difficult to distinguish between intersection and veering just by observing eigenvalue plots.Curve veering/crossing complexity obstructs the tracing of eigenvalue loci under parameter changes. Also, when multiple curves veer or intersect close together (Fig. 3), strong modal coupling and the associated operating condition response changes that occur are not identifiable from frequency loci plots.
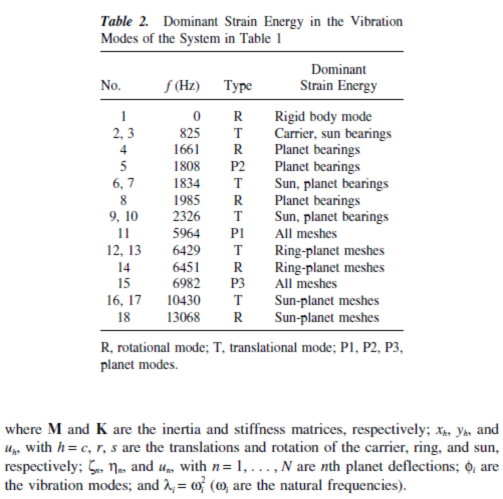
The objectives of this work were twofold. The first was to analytically derive simple rules that predict eigenvalue veering in planetary gears. The second was to use the veering results, along with previously developed modal properties and eigensensitivity analysis, to define more fully the influence of model parameters on free vibration and to give guidance for tuning natural frequencies.Lin and Parker [10,11] analytically characterized the unique, highly structured properties of planetary gear natural frequency spectra and vibration modes. They also provided simple, closed-form expressions for the sensitivities of natural frequencies and vibration modes to design parameters [12]. These analytical results provide the necessary foundation for the present study of veering rules in planetary gears. The veering rules yield concrete conclusions expressed in simple forms for when two approaching eigenvalues veer or cross. The importance of the veering rules is to identify those ranges in which small changes in design parameters can dramatically change the vibration modes and consequently the response. The results are illustrated on a benchmark planetary gear(the model parameters and natural frequencies are given in Tables 1 and 2,respectively) used in a helicopter power train.
The lumped parameter model derived in Ref. 10 is used here. The model is applicable for general epicyclic gears with N planets. Each component has two translational and one rotational degree of freedom (DOF) in planar motion,so the system has L=3(N-3) DOF. Numerical results presented are for fixedring configurations, and L=3(N-2) in this case. The associated eigenvalue problem is
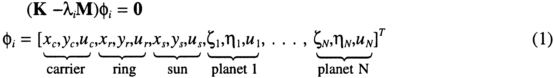

II. VEERING/CROSSING CRITERION
A method for detecting eigenvalue veering/crossing in general dynamic systems is introduced here. Point B in Fig. 2a is an example of veering. When two eigenvalue loci veer away, their loci curvatures indicate the abruptness of curve direction changes. Perkins and Mote [7] proposed a veering/crossing criterion by estimating the loci curvature in the veering neighborhood for distinct eigenvalues. Let 
 r and λs be two eigenvalues approaching each other around point B as a parameter r is varied. The unperturbed eigensolutions at B are (λr,Φr) and (λs,Φs). Applying Taylor expansion around B, the eigenvalue loci are approximated by
r and λs be two eigenvalues approaching each other around point B as a parameter r is varied. The unperturbed eigensolutions at B are (λr,Φr) and (λs,Φs). Applying Taylor expansion around B, the eigenvalue loci are approximated by
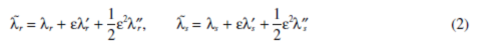
where å is a small perturbation of the varying parameter;λ¢=¶λ/¶r;λ¢¢=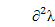
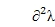 .The second derivatives λ¢¢r andλ¢¢s represent the curvatures of the loci.If λ¢¢r =λ¢¢s=0, these two loci are locally independent and free to cross each other. Ifλ¢¢r , λ¢¢s ¹0, the loci diverge and veering occurs. Larger λ¢¢ indicates sharper changes of the loci and stronger veering. For a distinct eigenvalueλr,the eigenvalue derivatives are
.The second derivatives λ¢¢r andλ¢¢s represent the curvatures of the loci.If λ¢¢r =λ¢¢s=0, these two loci are locally independent and free to cross each other. Ifλ¢¢r , λ¢¢s ¹0, the loci diverge and veering occurs. Larger λ¢¢ indicates sharper changes of the loci and stronger veering. For a distinct eigenvalueλr,the eigenvalue derivatives are
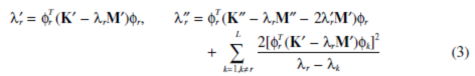
In the veering vicinity whereλr≈λs, λ¢¢r andλ¢¢s are dominated by terms with a small denominator, that is,
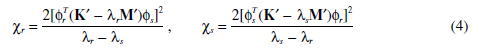
The coupling factors cr and cs approximate the local curvatures. They are used to estimate veering strength.
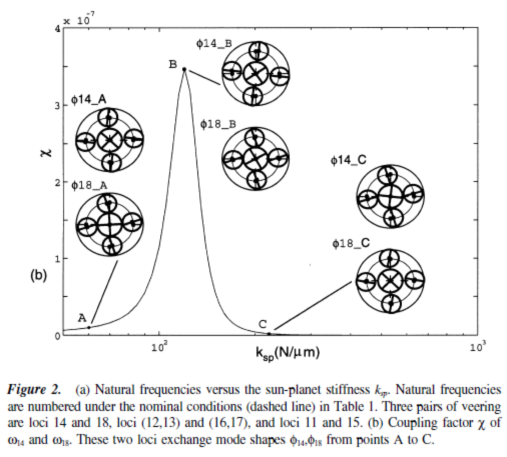
Figure 2b shows c =c14=c18 versus the varying parameter ksp for the veering loci w14 and w18 in Fig. 2a. Notice the sharply changing vibration modes indicated in Fig. 2b. The two veering loci exchange mode shapes from points A to C, even though the loci do not intersect. The modes are strongly coupled at B and do not look like either of the veering modes just outside the veering zone. When the parameter is adjusted in the veering zone, the drastic changes in the vibration modes can have a great impact on the operating condition dynamic response, tooth loads, load sharing, and bearing forces and possibly lead to mode localization. The degree to which individual modes are excited by dynamic mesh forces (i.e., the modal forces) also changes dramatically as veering alters the modes.
This veering criterion can be generalized to the case whenλs…λs+m-1 are degenerate with multiplicity m.The second derivatives of these eigenvalues are [14]
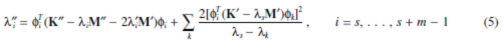
where the summation index k=1,… L, but k ¹s,…, s + m-1. When another distinct eigenvalue λr is close to the degenerate λi, the dominant terms in Eqs. 5 and 3 are
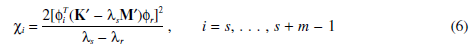

If λr …λr+n-1 is also degenerate, the coupling factors are
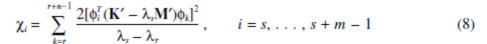
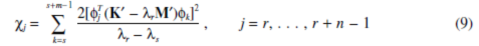
If the coupling factors are all zero, λr andλs loci cross; otherwise, veering occurs. This is the condition we examine below.
III. VEERING PATTERNS IN PLANETARY GEARS
When applied to planetary (or any epicyclic) gears, the above results reduce to particularly simple forms because of the unique structure of the vibration modes. All planetary gear vibration modes can be classified as one of the following types under the assumption of cyclic symmetry between the planets [10].The analysis is restricted to this commonly used class of epicyclic gears.
1. Six rotational modes with distinct natural frequencies. They have pure rotation of the carrier, ring, and sun, that is, xh =yh =0, h=c, r, s. All planets have the same deflection
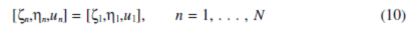
2. Six pairs of translational modes with degenerate natural frequencies of multiplicity two. They have pure translation of the carrier, ring,and sun, that is, uh = 0, h=c, r, s. For a pair of orthonormal translational modes Φi=and=Φj=(
 MΦj=0),
MΦj=0),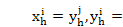
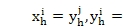 ,where the superscripts i and j indicate the modes Φi and Φj,respectively. The planet deflections have the relation
,where the superscripts i and j indicate the modes Φi and Φj,respectively. The planet deflections have the relation
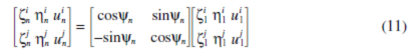
where Yn=2(n-1)
 /N for equally spaced planets.
/N for equally spaced planets.
3. Three groups of planet modes with degenerate natural frequencies of multiplicity N -3. They have no motion of the carrier, ring, and sun,that is, xh=yh=uh=0, h=c,r, s.The planet deflections are related by
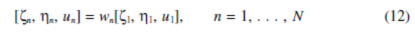
Where wn are N- 3 independent sets of scalars satisfying 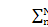
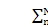 nsinYn
nsinYn
 ,
,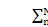
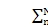 ncosYn
ncosYn
 ,
,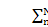
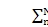 n=0
n=0
Two approaching planetary gear loci can be associated with any of the above three types of modes. Five cases of potential veering are examined below. The unique modal properties of Eqs. 10–12 were used to analyze the veering patterns. For concreteness, let the sun-planet mesh stiffness ksp be the varying parameter (Fig. 1) and M¢= 0.
Case 1. Two rotational mode loci λr and λs. Rotational modes have distinct eigenvalues, and their second derivative with respect to ksp is [12]

where dsn = yscos(Yn - as) - xssin(Yn -as) - hncosas -znsinas + us + un is the modal deflection of the spring representing the nth sun-planet mesh stiffness; as is the pressure angle of the sun-planet mesh; and the superscripts r and k in dsn indicate vibration modes jr and jk, respectively. The modal strain energy in the nth sun-planet mesh is d¢sn= ksp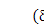
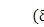 /2. The rotational mode property of Eq. 10 results in
/2. The rotational mode property of Eq. 10 results in 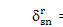
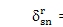 ,
,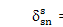
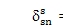 .The coupling factors of Eq. 4 are the dominant terms in Eq. 13
.The coupling factors of Eq. 4 are the dominant terms in Eq. 13
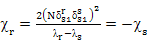
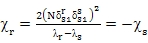 (14)
(14)
If 
 ,
,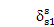
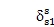 then cr, cs 0, and the approaching eigenvalue loci veer away.If
then cr, cs 0, and the approaching eigenvalue loci veer away.If 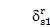
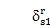 or
or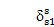
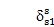 , then cr=cs=0, and the loci cross each other. This requires that all strain energy in the sun-planet meshes Usn = 0 for vibration mode
, then cr=cs=0, and the loci cross each other. This requires that all strain energy in the sun-planet meshes Usn = 0 for vibration mode 
 r or js. However, all rotational modes except the rigid body mode must have strain energy in the sun-planet meshes. Therefore, two rotational mode loci (e.g., w14 and w18 in Fig. 2a) always veer away and do not intersect. Also, more strain energy in the sun-planet meshes means larger cr and cs and sharper veering. Both loci have comparable curvatures, as indicated by cr -cs; this is typical of results to follow as well.
r or js. However, all rotational modes except the rigid body mode must have strain energy in the sun-planet meshes. Therefore, two rotational mode loci (e.g., w14 and w18 in Fig. 2a) always veer away and do not intersect. Also, more strain energy in the sun-planet meshes means larger cr and cs and sharper veering. Both loci have comparable curvatures, as indicated by cr -cs; this is typical of results to follow as well.
Case 2. Two translational mode loci λr=λp and λs =λq. Reducing Eq. 5 using the properties of translational modes, the derivatives λ¢¢r andλ¢¢p have the same form as Eq. 13, except the summation index k =1, …,L, but k¹r, p. The coupling factors of Eqs. 8 and 9 are the dominant terms inλ¢¢:
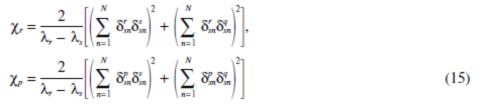
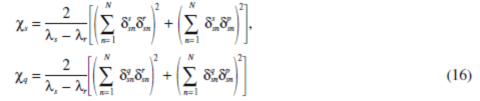
The translational mode property of Eq. 11 leads to the relations
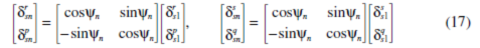
Use of Eq. 17 in Eqs. 15 and 16 yields
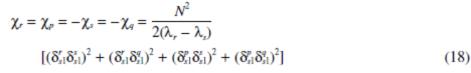
Vanishing of the coupling factors (that is, loci crossing) requires 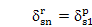
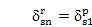 or
or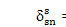
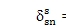 =0 for all n. Physically, this implies no strain energy in any sun-planet meshes for the translational mode pairs (jr,jp) and (js,jq). This does not occur,and the loci always veer away with strength determined bycr and cs (e.g., w12,13 and w16,17 in Fig. 2a).
=0 for all n. Physically, this implies no strain energy in any sun-planet meshes for the translational mode pairs (jr,jp) and (js,jq). This does not occur,and the loci always veer away with strength determined bycr and cs (e.g., w12,13 and w16,17 in Fig. 2a).
Case 3. A rotational mode locus λr and a translational mode locus λs =λq.From
Eqs.6and7,the coupling factors are
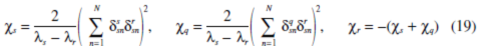
Recalling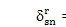
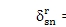 and Eq. 17, cs= cq=cr= 0 is automatically satisfiedbecause
and Eq. 17, cs= cq=cr= 0 is automatically satisfiedbecause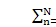
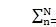 Yn
Yn
 ,
,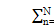
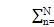 Yn
Yn
 0. Note there is no condition on any dsn, which is different from the above cases. A rotational mode locus always crosses a pair of
0. Note there is no condition on any dsn, which is different from the above cases. A rotational mode locus always crosses a pair of
translational mode loci without veering. By similar analyses, planet mode loci always cross rotational and translational mode loci.
Case 4. Two planet mode loci λr =λr+m-1 and
 s=λs+m-1 with multiplicity =3(N -3). The second derivatives of λr, … λr+m-1 have the form of Eq. 13, except the summation index k =1,… L, but k¹r,… , r +m-1. The coupling factors of Eqs. 8 and 9 are
s=λs+m-1 with multiplicity =3(N -3). The second derivatives of λr, … λr+m-1 have the form of Eq. 13, except the summation index k =1,… L, but k¹r,… , r +m-1. The coupling factors of Eqs. 8 and 9 are
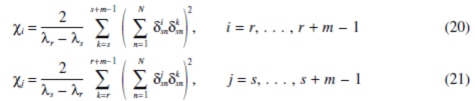
VEERING IN PLANETARY GEARS
Equating these coupling factors to zero yields the conditions for the absence of curve veering:
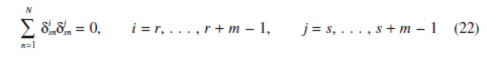
Using the planet mode property of Eq. 12, the sun-planet mesh deformations are related by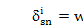
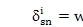 and
and 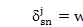
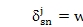 .Equation 22 results in
.Equation 22 results in
 0,i=r, …,r+ m-1 or
0,i=r, …,r+ m-1 or 
 0, j =s, …, s=m-1. Physically, these conditions require that one set of degenerate planet modes have no strain energy in the sun-planet meshes. This does not occur, in general. Therefore, the coupling factors of two planet modes are nonzero, and their loci veer away (e.g., w11 and w15 in Fig. 2a), except for the special case discussed below.
0, j =s, …, s=m-1. Physically, these conditions require that one set of degenerate planet modes have no strain energy in the sun-planet meshes. This does not occur, in general. Therefore, the coupling factors of two planet modes are nonzero, and their loci veer away (e.g., w11 and w15 in Fig. 2a), except for the special case discussed below.
Case 5. Two decoupled planet mode loci approach each other as kp, mp,or Ip is varied. For the case when ksp = krp and the pressure angle ar=as=a, the three planet modes have additional properties besides Eq. 12 and can be further classified as follows [10]: (1) mode P1 only has planet tangential motion hn (zn= un=0); (2) mode P2 has no tangential motion (hn= 0), and planet radial motion is dominant (zn=un); (3) mode P3 has no tangential motion (hn=0),
and planet rotation is dominant (zn=un). Note planet mode P1 always decouples from P2 and P3. If the pressure angle a=0, modes P2 and P3 also decouple, that is, u=0 in P2 and zn=0 in P3. With these additional properties, two decoupled planet mode loci can intersect. As an example, kp is taken as the varying parameter. The second derivative of a degenerate planet mode eigenvalue λr… λr+m-1 is [12]
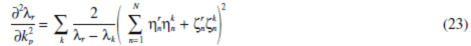
where the summation index k=1,…, L, but k ¹r,…, r + m- 1. The coupling
factors are
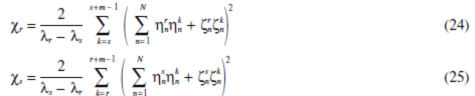
If λr is of type P1 andλs is of type P2 or P3, then cr = cs = 0 is guaranteed because
 =0, i = r,… r + m-1 and
=0, i = r,… r + m-1 and 
 =0, j= s,… s + m-1. So the mode P1 locus crosses the P2 and P3 loci (e.g., w11 and w15 intersect in Fig. 3 where ksp = krp andar = as). However, the mode P2 and P3 loci (w5 and w15 in Fig. 3) veer away because they are coupled when a¹0. If the conditions ksp =krp and ar=as are not satisfied, the three coupled planet modes veer away as discussed in case 4.
=0, j= s,… s + m-1. So the mode P1 locus crosses the P2 and P3 loci (e.g., w11 and w15 intersect in Fig. 3 where ksp = krp andar = as). However, the mode P2 and P3 loci (w5 and w15 in Fig. 3) veer away because they are coupled when a¹0. If the conditions ksp =krp and ar=as are not satisfied, the three coupled planet modes veer away as discussed in case 4.
The above analysis (cases 1–4) uses ksp as the varying parameter and shows that two eigenvalue loci of the same mode type veer away and two loci of different mode types intersect with each other. This pattern is generally valid when other parameters (either stiffness or inertia) are varied. For changing stiffness (ksp, krp, kp, kh, khu, h=c, r, s), the eigenvalue derivatives are related to the deflections d in the springs representing the stiffness [12]. If two loci have the same mode types, as in cases 1, 2, and 4 above, the coupling factor c=0 always requires the corresponding deflection d= 0 in the vibration modes. This requirement is unlikely to be satisfied except for the special situation discussed in case
5. Thus, c¹0 for two close loci of the same type and veering occurs. If two loci belong to different mode types as in case 3, c = 0 is automatically satisfied due to the modal properties of Eps. 10–12, and the loci always intersect. For changing inertia (mh, Ih, h=c, r, s, p), the analysis is similar to that for stiffness. The general veering/crossing patterns are summarized in Table 3 and are apparent in the example of Fig. 4 (in which the parameters are different from those in Fig. 2).
IV. APPLICATION
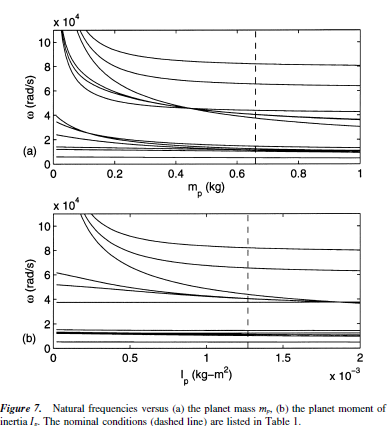
The veering patterns help trace the evolution of eigenvalue loci and identify the effects of design parameters on planetary gear vibration. The planetary gear in a helicopter power train is used as an example. The nominal model parameters are given in Table 1. Table 2 identifies the mode type and where the dominant strain energy is in each mode. The natural frequencies are numbered at the nominal conditions (indicated by the dashed lines in Figs. 2–7).
Mesh stiffnesses ksp and krp (Figs. 2 and 5) have little influence on the low
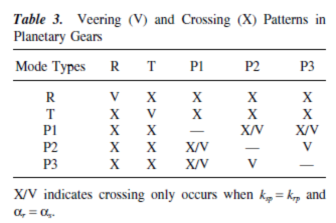
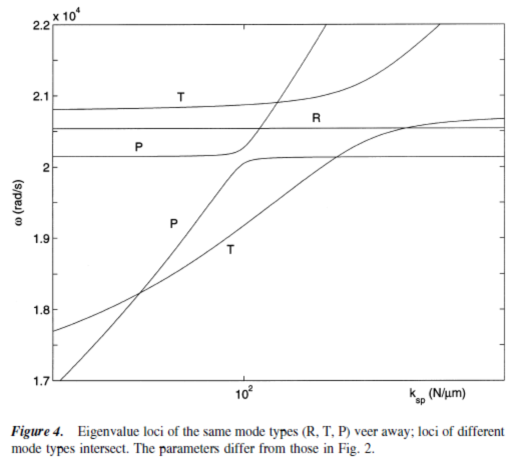
natural frequencies w1 ~ w10. This is because these modes are governed by bearing stiffnesses (Table 2) that are much smaller than the mesh stiffnesses. Modes 15–18 have large strain energy in the sun-planet meshes and are affected by ksp (Fig. 2); modes 11–14 have substantial strain energy in the ring-planet meshes and are affected by krp (Fig. 5). When ksp is reduced from the nominal value, the changingw15 to w18 approach the 
 11 to w14 loci. Because loci of the same type cannot intersect, veering occurs between rotational modes 18 and 14, translational mode pairs (16,17) and (12,13), and planet modes 15 and 11. Below the veering zones (ksp < 100N/mm), modes 11 to 14 are very similar to modes 15 to 18 above the veering zones (ksp > 800N/mm). In the same way, one can predict the trend of frequency loci as krp is increased (Fig. 5).
11 to w14 loci. Because loci of the same type cannot intersect, veering occurs between rotational modes 18 and 14, translational mode pairs (16,17) and (12,13), and planet modes 15 and 11. Below the veering zones (ksp < 100N/mm), modes 11 to 14 are very similar to modes 15 to 18 above the veering zones (ksp > 800N/mm). In the same way, one can predict the trend of frequency loci as krp is increased (Fig. 5).
Support stiffnesses kh, khu, and h = c, r, s of the carrier, ring, and sun, respectively, can vary over a wide range depending on the configuration (fixing or floating these components). Rotational and planet modes are independent of the transverse support stiffness kh because they have no translation of the carrier,
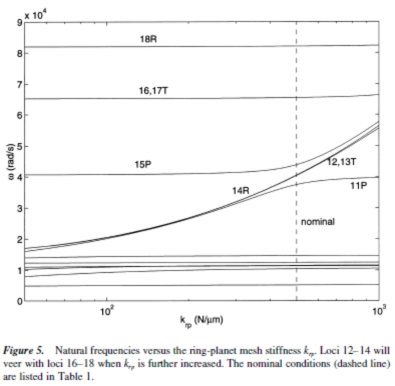
ring, and sun: only translational modes are affected by changes in kh (Figs. 6a,6b). When the rotational support stiffnesses khu are altered, similar results are obtained (Figs. 6c, 6d), except it is the rotational modes that are susceptible to khu variations.
Altering planet parameters affects most natural frequencies as all modes generally involve planet deflections. Applying the derived veering results, five pairs of veering are identified for changing planet bearing stiffness in Fig. 3: rotational modes 8 and 18, 4 and 14; translational modes (9,10) and (16,17),(6,7) and (12,13); and planet modes 5 and 15. For large stiffness kp > 5000N/mm, eight natural frequencies increase rapidly to outside the range of interest.Planet mass mp and moment of inertia Ip also have significant influence on the natural frequencies (Fig. 7).
V. DISCUSSION AND SUMMARY
The planets can be unequally spaced in planetary gear applications. For Planetary gears with planet position angles Yn satisfying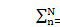
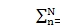 Yn
Yn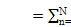
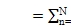 Yn
Yn
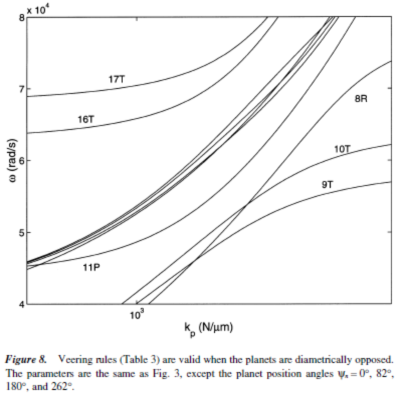
 0, the vibration modes retain structured properties [11]: 6 distinct rotational modes, 12 distinct translational modes, and 3 planet modes with multiplicity N-3. The translational modes become distinct because of the loss of cyclic symmetry. Under these conditions, the veering patterns in Table 3 still apply,although the analytical loci curvatures have a more complicated form. A practically important case has diametrically opposed planets with position angles Yn+N/2 = Yn + π. Figure 8 shows a four-planet example with Yn=0,82,180,262,while
0, the vibration modes retain structured properties [11]: 6 distinct rotational modes, 12 distinct translational modes, and 3 planet modes with multiplicity N-3. The translational modes become distinct because of the loss of cyclic symmetry. Under these conditions, the veering patterns in Table 3 still apply,although the analytical loci curvatures have a more complicated form. A practically important case has diametrically opposed planets with position angles Yn+N/2 = Yn + π. Figure 8 shows a four-planet example with Yn=0,82,180,262,while 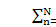
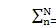 Yn
Yn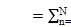
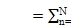 Yn
Yn
 0 other parameters remain the same as in prior figures. Translational modes 9 and 10, which are degenerate for equal planet spacing, cross the rotational mode 8, but veer away from translational modes 16 and 17. When planets
0 other parameters remain the same as in prior figures. Translational modes 9 and 10, which are degenerate for equal planet spacing, cross the rotational mode 8, but veer away from translational modes 16 and 17. When planets
are arbitrarily spaced, the vibration modes lose the structured properties of Eqs.10–12, so the derived veering patterns are not valid.
Eigenvalue loci veering also occurs when degenerate modes of a symmetric system are separated by small disorders. In planetary gears, the cyclic symmetry can be broken by differing mesh stiffnesses at each planet mesh, manufacturing variations, and assembly errors. For cyclically symmetric or periodic systems with small disorders and weak structural coupling, mode localization often accompanies eigenvalue loci veering [6]. Planetary gears have relatively strong coupling between the planets through the carrier and teeth meshes, so sharp mode localization is unlikely even in the presence of loci veering. After
examination of many cases with various configurations and parameters, we have not found a realistic example of mode localization in planetary gears.
The special veering patterns of planetary gear eigenvalue loci are easily summarized. Two approaching eigenvalue loci of the same type (rotational mode, translational mode, and planet mode) veer away, while two loci of different mode types cross each other. The mode shapes are exchanged across the veering zone. In the veering zone, the modes are strongly coupled and markedly different from outside the zone. One can expect significant differences in response from these changed modes. These rules result from the unique modal properties of the planetary gears and apply to all design parameters. The characterized veering patterns, combined with the unique modal properties and the eigensensitivity analysis, provide considerable insight into planetary gear free vibration.
The effects of key design parameters are summarized below:
1. Mesh stiffness. ksp and krp each control three different natural frequencies associated with one rotational mode, one pair of translational modes, and one group of planet modes. Dominant strain energy occurs in the tooth meshes of these vibration modes.
2. Carrier, ring, and sun parameters. kh and khu, h= c, r, s, each affect only one natural frequency. The transverse stiffness kh controls one pair of translational modes, and the torsional stiffness khu controls one rotational mode. Floating or fixing the carrier, ring, or sun has limited influence on planetary gear modal properties. The carrier, ring, and sun masses and moments of inertia affect the same frequencies as their corresponding support stiffness, although the frequencies vary in the opposite direction.
3. Planet parameters. Planet bearing stiffness and planet inertia are the most influential parameters and affect most natural frequencies. A stiff planet bearing can be beneficial for resonance tuning because it substantially reduces the number of natural frequencies in the lower frequency range that is commonly of most interest.