目 录

1 问题描述

2 需求分析

2.1 数据需求

2.2 功能需求

3 概要设计

3.1 主体设计

3.2 用户界面设计

3.3抽象数据类型

3.3.1 科学计算器

3.3.2 多项式计算器

3.3.3 历史记录

3.4 功能模块设计

3.4.1 科学计算器

3.4.2多项式计算器:

3.4.3.历史记录

4 详细设计及系统实现

4.1 科学计算器

4.1.1 科学计算器数据结构

4.1.2 科学计算器界面

4.1.3 科学计算机算法实现

4.2多项式计算器

4.2.1 多项式计算器数据结构

4.2.2 多项式计算器界面

4.2.3多项式计算器算法实现

4.3  历史记录

4.3.1 历史记录数据结构

4.3.2 历史记录界面

4.4 程序打包

5 系统调试分析

6 课程设计总结

6.1实现功能

6.2有待改进部分

6.3自我总结

附录：

1 问题描述

设计程序模拟Windows计算器,部分要求如下:

<1>为计算器设计

<2>计算器可以进行基本的计算

<3>计算器可以识别括号,并对常见函数如幂函数、三角函数、对数函数等进行求解

<4>计算器能够保存历史运算表达式,用户可以查看历史运算

<5>计算器可以实现一元多项式的运算

例：设有一元多项式Am(x)和Bn(x)：

Am(x)=A0+A1x1+A2x2+A3x3+… +Amxm,

Bn(x)=B0+B1x1+B2x2+B3x3+… +Bnxn.

可求得M(x)= Am(x)+Bn(x)、M(x)= Am(x)-Bn(x)和M(x)= Am(x)×Bn(x),

且M(x)中无重复阶项和无零系数项，并且输出结果有升幂和降幂两种排列情况。

2 需求分析

该演示程序在Python的tkinter库环境中编写,目标是实现一个包含多项式运算功能的科学计算器.

2.1 数据需求

<1>输入数据的形式和范围:在进行普通运算时,数据从按键上输入.在进行多项式运算时,多项式从键盘输入,并通过下拉框选择合适的运算符号进行运算.

<2>输出形式:在输出框内显示运算结果.若输入算式有误,给予用户提示.

2.2 功能需求

<1>需要对Python软件与对应语法具备一定了解.

<2>需要具备基本的编程能力,需了解各个计算器按键的功能.

<3>需要熟练运用正则表达式进行字符串匹配.

3 概要设计

3.1 主体设计

图3.1.1计算器功能全局流程

3.2 用户界面设计

<1>科学计算器界面:需包含绝大多数科学计算器中按键,并可通过点击按键引起输入框中的文本变化,同时需要创建多项式计算按键与历史记录查看按键,在呈现简洁性的同时方便用户操作.

<2>多项式计算器界面:需包含两个输入框,用于输入待计算多项式,同时设置符号选择框,限制可用于进行的多项式运算操作.此外,还需设置两个输出框(一个升幂输出,一个降幂输出)和一个历史记录显示按键.

<3>历史记录界面:需包含文本展示框与文本清除按钮.

3.3抽象数据类型

3.3.1 科学计算器

calculator = Tk()
calculator.title("Calculator")

3.4 功能模块设计

3.4.1 科学计算器

1.确定科学计算器按键及其功能.

2.设置基本运算符对应的元数(实现)

3.当输入”=”后,通过正则表达式,将输入中的运算符和操作数区分开,并将划分好的子串临时储存在向量中.

4.从向量起始位置到末尾,依次判断元素.若该元素为操作数,入操作数栈;若该元素为运算符时,则判断其能否进运算符栈.判断规则如下:

(1)运算符栈底压入”#”.

(2) 若运算符包含”(”,直接进栈

(3) 若运算符不为”)”且不包含”(”,首先判断该运算符是否为”-”.若是,判断该减号位置.若其位于表达式起始处或者向量中减号前一位置元素包含”(”,在操作数栈中压入0.此后判断该运算符与运算符栈顶符号的优先级.若该运算符优先级大于栈顶元素,该运算符入栈;否则栈顶元素出栈并进行对应操作:若为一元运算符,操作数栈出栈一个数,处理后进操作数栈;若为二元运算符,操作数栈出栈两个数,处理后进操作数栈.

(4)若运算符为”)”,运算符栈和操作数栈持续执行(2)中对应操作,直至扫描到一个运算符包含”(”,该运算符再出栈执行(2)对应操作.

(5)扫描到”#”,若表达式正确,则代表算式计算完成,操作数栈栈顶元素即为所求.

5.将操作数栈顶元素出栈,写入输出框,同时将整个算式写入历史记录中.

6. 计算过程中,要对部分可能出现异常进行处理:

(1)括号需匹配

(2)log,ln函数的底数部分需大于0且不等于1,指数部分需大于0

(3)偶次幂根号下数字需大于0

(4)除数不能为0

(5)任何数的0次幂为1

7.字母表达式(运算符)都以”(”结尾,其运算也同括号规律相同.

8.向量实现减号取负方式:

若减号为初始位or减号前一位存在括号

操作数栈压入0

此后减号继续当作二元运算符使用即可

3.4.2多项式计算器:

1. 给出输入示例,避免由于异常输入导致结果异常.

2.输入两个多项式后选择对应运算符,点击”Compute”按键开始计算,对每一个多项式的操作步骤如下:

(1)利用正则表达式将多项式拆分成特定结构的单项式,每个单项式入队列

(2)依次对每个单项式进行以下操作:

<1> 将单项式拆分成系数符号、系数、变量、乘方号、幂次五部分(每一部分都允许缺失).

<2>拆分后对单项式进一步识别,获取其幂次和系数.

<3>以单项式的幂次为键(以下简称key),系数为值(以下简称value),构建键值对,并加入一个哈希表.

3.根据两个多项式的哈希表进行运算的过程如下:

判断运算符:

若运算符为”+”,获取表2中所有keys,并在表1中依次检索:

若表1中存在相同key,更新表1中该key对应的value值为当前值加表2中该key对应的value值.

若表1中不存在相同key,则在表1中添加表2中的<key,value>键值对.

若运算符为”-”,获取表2中所有key,并在表1中检索:

若表1中存在相同key,更新表1中该key对应的value值为当前值减去表2中该key对应的value值

若表1中不存在相同key,则在表1中添加对应的<key,-value>键值对

若运算符为”*”,新建哈希表3,并执行下述代码所示操作:

4.运算结果输出:

由于qt中哈希表默认按键升序排列,因此升幂输出即是按照表中键值对排列顺序输出,降幂输出即为逆序输出.同时要注意:第一位输出若为正数,不输出”+”号.编写输出规范时(两种输出方式通用),要兼顾所有形式的输出.

5.将算式与两种输出添加到历史记录中.

3.4.3.历史记录

在调用show()函数后出现,界面关闭前若未点击”CLC”,关闭后仍然保存算式记录.

4 详细设计及系统实现

该程序所有界面均在python中完成,并在界面初始化函数中进行了一定美化.

4.1 科学计算器

4.1.1 科学计算器数据结构

# 创建计算器界面
calculator = Tk()
calculator.title("Calculator")

4.1.2 科学计算器界面

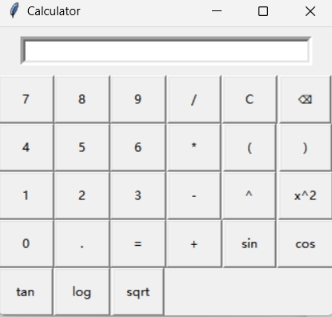
1.界面展示

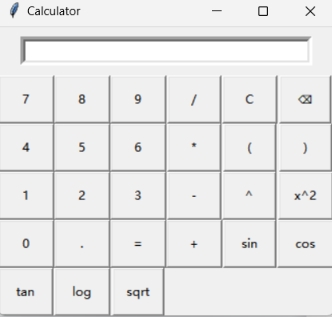
2.按键功能

3.界面实现

(1)界面组件:Python的Tkinter库

(2)在设计模式中,将组件调整大小后拖动到相应位置并命名

图4.1.2.5   初始科学计算器界面

4.1.3 科学计算机算法实现

def calculate(expression):
    try:
        result = eval(expression)
        history.append(expression)
        return result
    except:
        return "Invalid expression"

2.界面实现

(1)界面组件：Python的Tkinter库

(2)在设计模式中,将组件调整大小后拖动至合理位置并命名.

(1)设置按钮格式与槽函数.

(2)初始化组合框,添加可挑选符号+,-,*.

(3)更改标题,为历史记录按键添加图标.

(4)调整输入的文本字体大小,并设置右对齐

图4.3.2.1历史记录界面

2.界面实现:

(1)界面组件:Python的Tkinter库

(2)在设计模式中,拖动对应组件至合理位置并命名

(3)更改标题,调整输入记录的文本字体大小,并设置右对齐

6 课程设计总结

6.1实现功能

本计算器实现功能如下:

(1)可实现科学计算器的多数运算.

(2)可在一定程度上对异常算式进行错误处理.

(3)多项式计算器可按幂次无序输入,同时进行多项式的+,-,*运算.

(4)实现了历史记录,可查看历史算式.

6.2有待改进部分

本计算器有待改进部分如下:

(1)未能顾全所有异常输入,部分输入可能导致程序出错

(2)异常多项式没有很好的异常处理方式.

(3)历史记录界面制作相对粗略,可对其输入算式格式进行进一步美化.

(4)部分代码存在冗余.

(5)精度设置同系统计算器存在差异

6.3自我总结

本次课程设计是我上大学来完成的首个难度较高的程序设计.从总体设计到局部实现,从抽象逻辑到代码编程,我对基本的数据结构有了进一步了解,也初步掌握了界面设计的相关技能,认识到了合适的数据结构对算法实现的帮助.在完成负数运算时,需要对每一个减号的前一位进行判断.此时若使用栈或队列临时存储正则表达式匹配后的各个子串,在扫描到减号后是无法获取前一位数据的任何信息的.若使用数组临时储存,数组的大小又是未知的.因此选择使用向量作为临时存储结构是极为方便的.同时,在完成该课程设计过程中,我也对程序员平台CSDN,GitHub等有了初步了解,这对于我今后的学习无疑是有很大帮助的.我会牢记这次课设过程,从中吸取教训,并不断进步.

参考文献

附录：

源代码 : from tkinter import *
# 创建计算器界面
calculator = Tk()
calculator.title("Calculator")
# 创建输入框
input_box = Entry(calculator, width=40, borderwidth=5)
input_box.grid(row=0, column=0, columnspan=6, padx=10, pady=10)
# 定义按钮点击事件
def button_click(number):
    current = input_box.get()
    input_box.delete(0, END)
    input_box.insert(0, current + str(number))
def button_clear():
    input_box.delete(0, END)
def button_equal():
    expression = input_box.get()
    try:
        result = eval(expression)
        input_box.delete(0, END)
        input_box.insert(0, result)
    except:
        input_box.delete(0, END)
        input_box.insert(0, "Error")
def button_backspace():
    current = input_box.get()
    input_box.delete(0, END)
    input_box.insert(0, current[:-1])
# 创建按钮
button_1 = Button(calculator, text="1", padx=20, pady=10, command=lambda: button_click(1))
button_2 = Button(calculator, text="2", padx=20, pady=10, command=lambda: button_click(2))
button_3 = Button(calculator, text="3", padx=20, pady=10, command=lambda: button_click(3))
button_4 = Button(calculator, text="4", padx=20, pady=10, command=lambda: button_click(4))
button_5 = Button(calculator, text="5", padx=20, pady=10, command=lambda: button_click(5))
button_6 = Button(calculator, text="6", padx=20, pady=10, command=lambda: button_click(6))
button_7 = Button(calculator, text="7", padx=20, pady=10, command=lambda: button_click(7))
button_8 = Button(calculator, text="8", padx=20, pady=10, command=lambda: button_click(8))
button_9 = Button(calculator, text="9", padx=20, pady=10, command=lambda: button_click(9))
button_0 = Button(calculator, text="0", padx=20, pady=10, command=lambda: button_click(0))
button_add = Button(calculator, text="+", padx=19, pady=10, command=lambda: button_click("+"))
button_subtract = Button(calculator, text="-", padx=20, pady=10, command=lambda: button_click("-"))
button_multiply = Button(calculator, text="*", padx=20, pady=10, command=lambda: button_click("*"))
button_divide = Button(calculator, text="/", padx=20, pady=10, command=lambda: button_click("/"))
button_decimal = Button(calculator, text=".", padx=22, pady=10, command=lambda: button_click("."))
button_open_bracket = Button(calculator, text="(", padx=20, pady=10, command=lambda: button_click("("))
button_close_bracket = Button(calculator, text=")", padx=20, pady=10, command=lambda: button_click(")"))
button_exponent = Button(calculator, text="^", padx=18, pady=10, command=lambda: button_click("**"))
button_sin = Button(calculator, text="sin", padx=14, pady=10, command=lambda: button_click("sin("))
button_cos = Button(calculator, text="cos", padx=14, pady=10, command=lambda: button_click("cos("))
button_tan = Button(calculator, text="tan", padx=14, pady=10, command=lambda: button_click("tan("))
button_log = Button(calculator, text="log", padx=14, pady=10, command=lambda: button_click("log("))
button_sqrt = Button(calculator, text="sqrt", padx=10, pady=10, command=lambda: button_click("sqrt("))
button_power = Button(calculator, text="x^2", padx=12, pady=10, command=lambda: button_click("**2"))
button_equal = Button(calculator, text="=", padx=19, pady=10, command=button_equal)
button_clear = Button(calculator, text="C", padx=19, pady=10, command=button_clear)
button_backspace = Button(calculator, text="⌫", padx=14, pady=10, command=button_backspace)
# 将按钮放置在界面上
button_7.grid(row=1, column=0)
button_8.grid(row=1, column=1)
button_9.grid(row=1, column=2)
button_divide.grid(row=1, column=3)
button_clear.grid(row=1, column=4)
button_backspace.grid(row=1, column=5)
button_4.grid(row=2, column=0)
button_5.grid(row=2, column=1)
button_6.grid(row=2, column=2)
button_multiply.grid(row=2, column=3)
button_open_bracket.grid(row=2, column=4)
button_close_bracket.grid(row=2, column=5)
button_1.grid(row=3, column=0)
button_2.grid(row=3, column=1)
button_3.grid(row=3, column=2)
button_subtract.grid(row=3, column=3)
button_exponent.grid(row=3, column=4)
button_power.grid(row=3, column=5)
button_0.grid(row=4, column=0)
button_decimal.grid(row=4, column=1)
button_equal.grid(row=4, column=2)
button_add.grid(row=4, column=3)
button_sin.grid(row=4, column=4)
button_cos.grid(row=4, column=5)
button_tan.grid(row=5, column=0)
button_log.grid(row=5, column=1)
button_sqrt.grid(row=5, column=2)
# 创建一个空列表用于保存历史运算表达式
history = []
# 定义计算函数
def calculate(expression):
    try:
        result = eval(expression)
        history.append(expression)
        return result
    except:
        return "Invalid expression"
# 调用计算函数并保存历史运算表达式
result = calculate("2 + 3")
print(result)  # 输出：5
print(history)  # 输出：['2 + 3']
result = calculate("4 * 5")
print(result)  # 输出：20
print(history)  # 输出：['2 + 3', '4 * 5']
class Polynomial:
    def __init__(self, coefficients):
        self.coefficients = coefficients
    def add(self, other):
        result = []
        for i in range(max(len(self.coefficients), len(other.coefficients))):
            coeff1 = self.coefficients[i] if i < len(self.coefficients) else 0
            coeff2 = other.coefficients[i] if i < len(other.coefficients) else 0
            result.append(coeff1 + coeff2)
        return Polynomial(result)
    def multiply(self, other):
        result = [0] * (len(self.coefficients) + len(other.coefficients) - 1)
        for i, coeff1 in enumerate(self.coefficients):
            for j, coeff2 in enumerate(other.coefficients):
                result[i + j] += coeff1 * coeff2
        return Polynomial(result)
    def evaluate(self, x):
        result = 0
        for i, coeff in enumerate(self.coefficients):
            result += coeff * (x ** i)
        return result
    class Polynomial:
        def __init__(self, coefficients):
            self.coefficients = coefficients
        def add(self, other):
            result = []
            for i in range(max(len(self.coefficients), len(other.coefficients))):
                coeff1 = self.coefficients[i] if i < len(self.coefficients) else 0
                coeff2 = other.coefficients[i] if i < len(other.coefficients) else 0
                result.append(coeff1 + coeff2)
            return Polynomial(result)
        def multiply(self, other):
            result = [0] * (len(self.coefficients) + len(other.coefficients) - 1)
            for i, coeff1 in enumerate(self.coefficients):
                for j, coeff2 in enumerate(other.coefficients):
                    result[i + j] += coeff1 * coeff2
            return Polynomial(result)
        def evaluate(self, x):
            result = 0
            for i, coeff in enumerate(self.coefficients):
                result += coeff * (x ** i)
            return result
# 运行计算器
calculator.mainloop()